Analyse Chikwadraattoets

Met deze toets probeer je aannemelijk te maken dat er verschil bestaat tussen groepen wat betreft een bepaald kenmerk.
Dit voorbeeld is overigens ook grafisch uitgewerkt.

De uitvoering is in een aantal stappen te onderscheiden:

• Hypothesen
• Uitvoering met behulp van SPSS
• De uitvoer van SPSS
• Controle op voorwaarden
• Interpretatie van de uitvoer
• Slotopmerkingen
• Het voorbeeldbestand bij de Chikwadraattoets

In een aantal wijken van Arnhem en Nijmegen is onderzoek gedaan naar het internetgebruik van de bewoners van die wijken (voorjaar 2004). Eén van de gestelde subvragen was of er verschil in internetgebruik was tussen de woonwijken.

Heel gebruikelijke hypothesen zijn hier:

H₀: Er is geen verschil tussen de wijken wat betreft internetgebruik
H₁: Er is wel verschil tussen de wijken wat betreft internetgebruik

Uitvoering met behulp van SPSS

Kies Crosstabs en neem de instellingen over van bijgevoegde figuren.

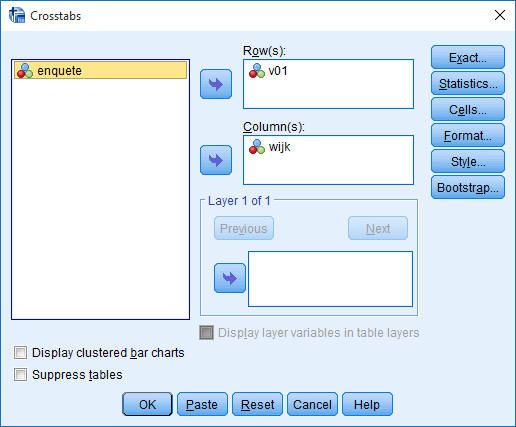
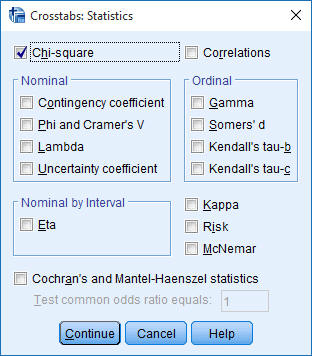
De uitvoer van SPSS

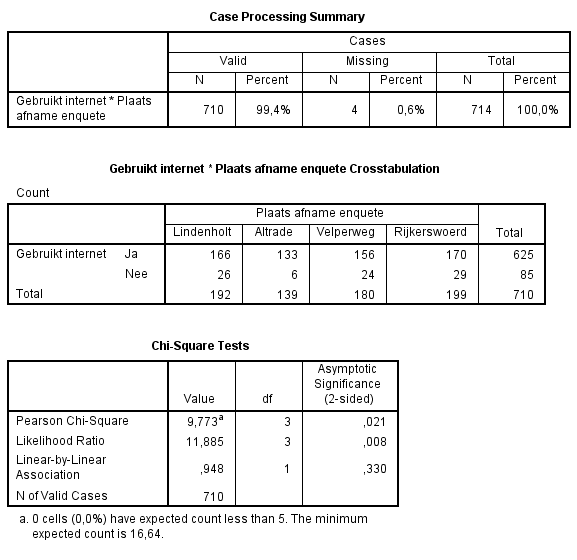
Controle op voorwaarden

Om de chikwadraattoets te mogen toepassen moet aan twee voorwaarden voldaan zijn. Deze zijn:

1. Hoogstens 20% van de verwachte frequenties is kleiner dan 5.
2. De minimale verwachte frequentie is minstens 1.

Controle:

1. Aflezen: 0% of the cells have expected counts less than 5, dus zeker minder dan 20 %!
2. Aflezen: the minimum expected count is 16,64, dus zeker meer dan 1!

Aan beide voorwaarden is voldaan. De chikwadraattoets mag daarom gebruikt worden.

Interpretatie van de uitvoer

De "Pearsons Chi-square" heeft een asymptotic, 2-sided, significance, ofwel een tweezijdige p-waarde van 0,021.
De conclusie zal op een tweetal verschillende manieren verwoord worden. Beide manieren betekenen echter hetzelfde.

• Er is dus een significant verschil (α = 2,1%) geconstateerd in het internetgebruik tussen de wijken.
• We kunnen met een betrouwbaarheid van 97,9% (=100% - 2,1%) H₀ verwerpen en H₁ accepteren en concluderen dat er een verschil in internetgebruik is tussen de wijken.

Slotopmerkingen

• Als niet aan de voorwaarden voldaan is kan via Recode, door klassen handig samen te voegen, toch voldaan worden aan de voorwaarden. Voor het gebruiken van de chikwadraattoets wordt er van uitgegaan dat de twee variabelen een nominaal meetniveau hebben.
• Als de variabelen een hoger een meetniveau hebben is het gebruiken van de chikwadraattoets niet fout, maar is wellicht een andere (verschil)toets geschikter.
• Betrouwbaarheden lager dan 90% zijn niet zo gebruikelijk.