Grafieken Boxplot

Een boxplot wordt gebruikt om snel een indruk te krijgen de verdeling van een variabele. Een boxplot voor een groep als geheel zegt niet zo heel veel, daarvoor is een boxplot niet specifiek genoeg. Een boxplot waarin groepen met elkaar vergeleken kunnen worden, kan wel heel nuttig zijn.

Deze pagina heeft de volgende opbouw:

• bespreking voorbeeld;
• het maken van een boxplot ;
• een uitleg van de elementen van een boxplot ;
• het bepalen van de kwartielen ;
• het maken van een boxplot met een uitsplitsing naar subgroepen ;
• conclusie en slotopmerkingen ;
• het gebruikte bestand .

Bespreking voorbeeld

In een groot onderzoek onder bachelorstudenten van de HAN in 2015 is onder andere gevraagd naar het geboortejaar van de respondent. Daarnaast moest men aangeven aan welke faculteit men studeerde. Die gegevens worden in dit voorbeeld gebruikt. De codering is als volgt:

Voor Faculteit_num (er zijn geen missings gedefinieerd):

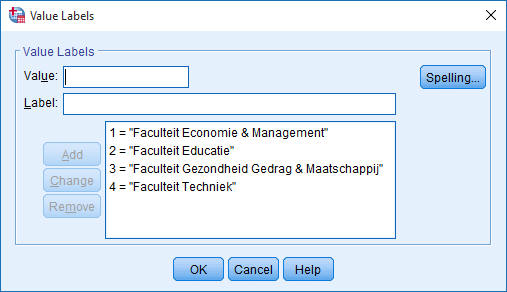
Voor geboortejaar:

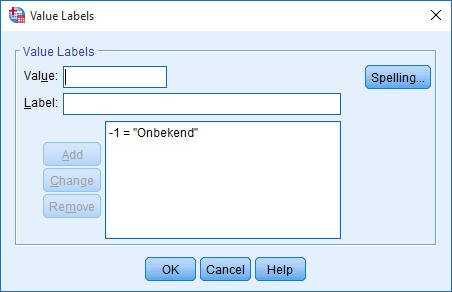
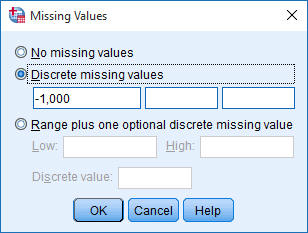
Het maken van een boxplot

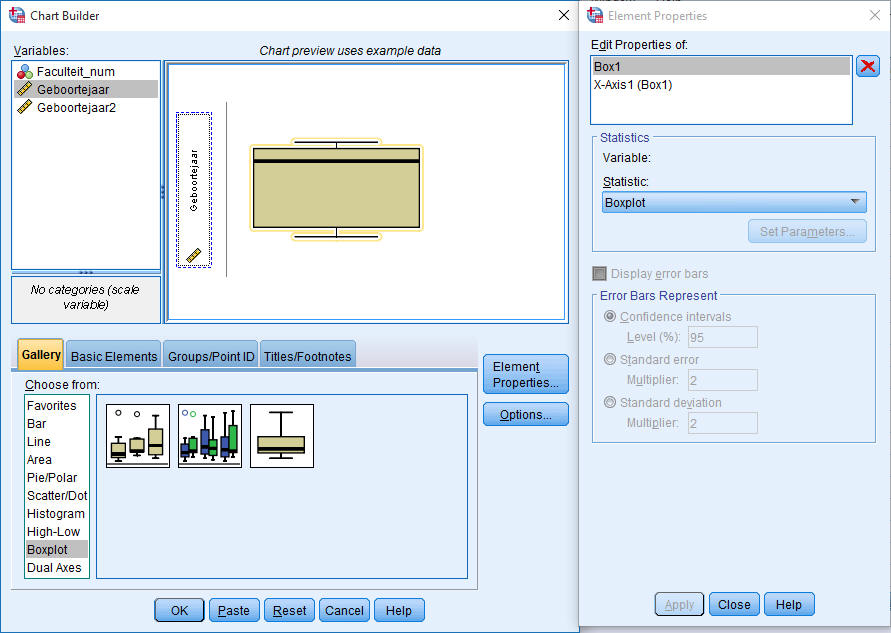
Het resultaat:

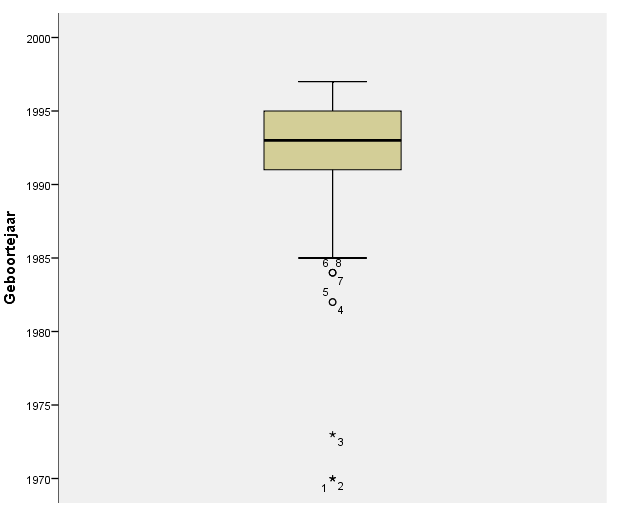
Nog geen erg prettig leesbare grafiek.

Een uitleg van de elementen van een boxplot

Deze grafiek is in SPSS aangepast tot (alleen de rode letters zijn later toegevoegd) :

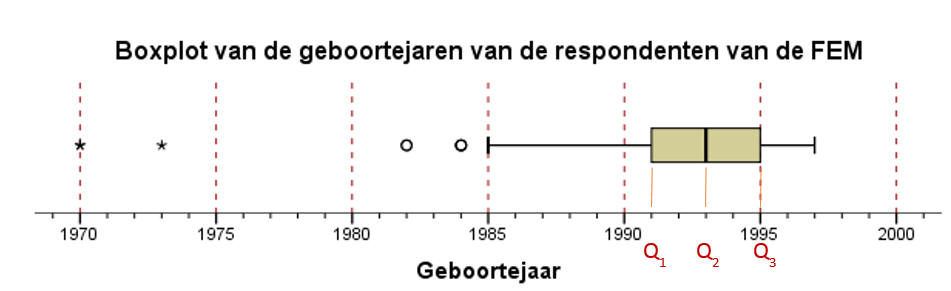
De betekenis van de elementen is als volgt:

*	Extreme
o	Outlyer
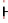
	Het uiteinde heet een whisker
Q1	Eerste kwartiel: hoogstens 25% van de antwoorden is kleiner en hoogstens 75% is groter
Q2	Tweede kwartiel = mediaan: hoogstens 50% van de antwoorden is kleiner en hoogstens 50% is groter
Q3	Derde kwartiel: hoogstens 75% van de antwoorden is kleiner en hoogstens 25% is groter

Om nu het plaatje te kunnen tekenen bepaalt SPSS eerst nog de interkwartielafstand = Q₃ - Q₁ .
Hier is dat dus 1995 - 1991 = 4.

Er zijn meerdere manieren om het plaatje te tekenen; soms wordt de complexiteit ook weggehaald. In deze uitleg wordt echter uitgegaan van de manier waarop SPSS de elementen bepaalt.

Vanaf Q₁ naar links kijkend zijn alle antwoorden kleiner dan Q₁ - 1,5 keer de interkwartielafstand een 'extreme' of een 'outlyer'. Antwoorden kleiner dan Q₁ - 3 keer de interkwartielafstand worden een 'extreme' genoemd. Dus antwoorden kleiner dan 1991 - 12 = 1979 zijn extremes, antwoorden vanaf 1979 tot 1985 zijn outlyers. De whisker wordt gezet op het laagste antwoord dat geen extreme of outlyer is, in dit geval is dat 1985.

Vanaf Q₂ naar rechts kijkend gaat het op dezelfde manier. Er zijn echter geen respondenten met een geboortejaar hoger dan 1995 + 1,5 keer de interkwartielafstand, dus er zijn geen outlyers en geen extremes. De rechter whisker staat bij 1997, wat het hoogste geboortejaar is.

Enkele conclusies uit bovenstaande boxplot:

• Ongeveer 50% van de respondenten heeft een geboortejaar van 1993 tot en met 1997
• In de geboortejaren voor 1991 zit redelijk veel spreiding, met enkele uitschieters (lage geboortejaren)

Het bepalen van de kwartielen

Bovenstaande houdt in dat Q₁, Q₂ en Q₃ bepaald worden en de rest van de figuur daardoor vastligt. Q₁, Q₂ en Q₃ zijn te bepalen via:

Dit levert de volgende twee tabellen: 

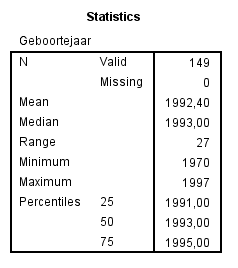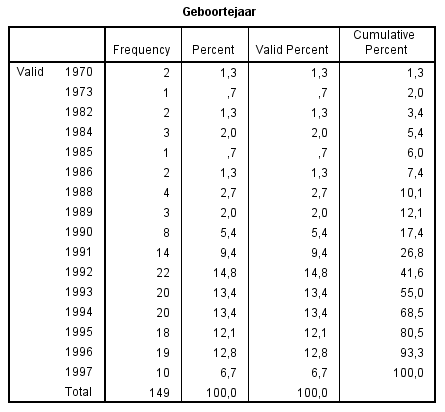
In de linker tabel zijn de kwartielen eenvoudig af te lezen.

In de rechtertabel kan dat via de Cumulatieve percentages. Als deze van boven naar beneden kijkend voor het eerst boven de 25% is, dan is het bijbehorende geboortejaar het eerste kwartiel. Net zo voor de mediaan (het tweede kwartiel) bij 50% en voor het derde kwartiel bij 75%. Je ziet dan ook dat slechts 19,5% van de respondenten 1996 of 1997 als geboortejaar heeft.

Het blok (de box) bevat hier overigens 63,1% (= 100% - 19,5% - 17,4%) van alle geboortejaren.

Het maken van een boxplot met een uitsplitsing naar subgroepen

Er wordt nu een boxplot gemaakt waarbij er uitgesplitst wordt naar faculteit.

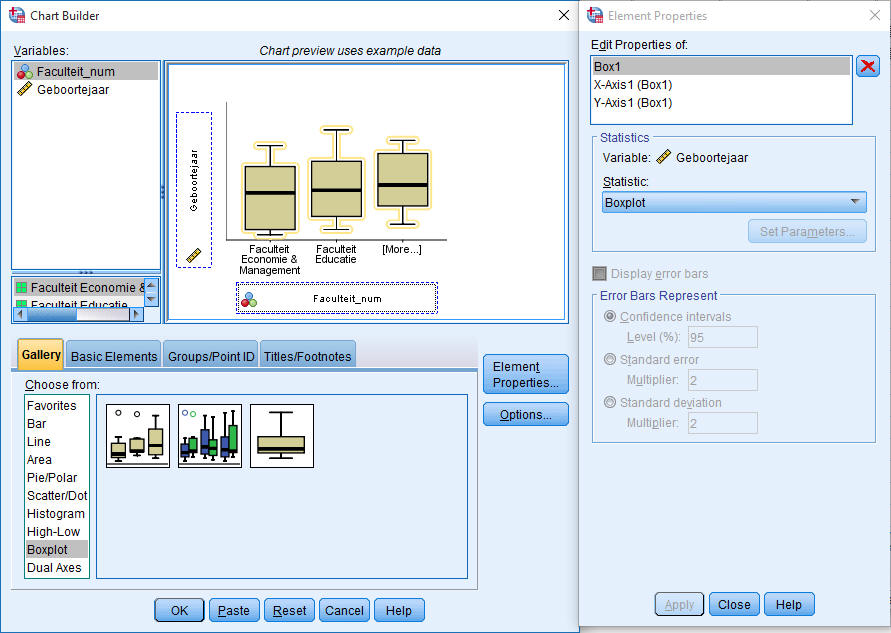
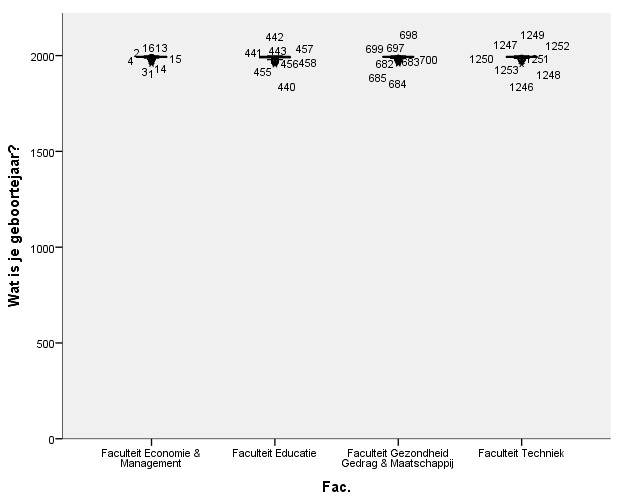
Dit ziet er echt niet uit. Na wat aanpassingen:

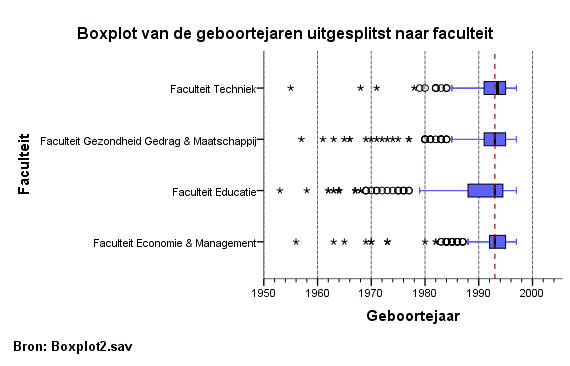
Wat valt er te concluderen?

Ligging: medianen allemaal 1993, alleen bij Techniek is die 1994. Het hoogste geboortejaar is bij alle faculteiten 1997.

Spreiding: de box bij Educatie is wel breder dan de andere boxen, daarom ligt de whisker ook verder naar links. De box bij Economie & Management is kleiner dan de andere drie. De spreiding in geboortejaren is bij Educatie groter dan bij de andere drie. Bij Economie & Management is die wat kleiner.

Aantallen uitschieters: Er zijn toch nog wel wat uitschieters (lage geboortejaren), terwijl de grootste groep (meer dan 75 % van de responenten per faculteit een geboortejaar heeft tussen van 1988 tot en met 1997).
Dat het aantal uitschieters bij Techniek kleinder is dan bij Educatie hoeft nog niet zoveel te zeggen, je weet namelijk niet hoeveel studenten er bij elke faculteit zitten.

Conclusie en slotopmerkingen

• Met een boxplot kun je redelijk snel verschillen in verdelingen onderscheiden.
• Een boxplot is wel een erg grove manier om de verdeling te laten zien: erg veel details worden weggelaten.
• Hoewel met kwartielen wordt gewerkt, is het meetniveau toch scale (interval) omdat er verschillen worden berekend. Bij ordinale variabelen worden wel eens boxplots gemaakt, maar is in feite  niet juist.
• In bovenstaand voorbeeld zijn er veel samenvallende waarden. Dat maakt de interpretatie ook minder nauwkeurig.