Analyse T-toetsen

Bij het vergelijken van gemiddelden in steekproeven wordt Compare Means gebruikt. Bij de procedure Means kunnen veel statistieken uitgerekend worden. De andere vier procedures bij Compare Means zijn toetsen waar op basis van gemiddelden uit steekproeven uitspraken gedaan kunnen worden over gemiddelden in populaties.

In de achterliggende theorie wordt ervan uitgegaan dat de steekproefverdelingen normaal verdeeld zijn. Of dat zo is moet eigenlijk steeds worden nagegaan. Bij kleine steekproeven (n < 30) kan dat door middel van een nonparametrische toets. Kies dan bijvoorbeeld voor de Kolmogorov-Smirnov toets. Bij grotere steekproeven (n >= 30) mag normaliteit worden aangenomen.

Wat kan er met elk van de vijf procedures die onder Compare Means vermeld staan gedaan worden?

• Means
• One-Sample T test
• Independent-Samples T Test
• Paired Sample T Test
• One-Way ANOVA

Means

Het voorbeeldbestand bij Means
Het voorbeeldbestand bevat schadebedragen bij ongelukken voor en na een aanpassing van een verkeerssituatie.

Met Means kan een aantal statistieken worden uitgerekend voor de schadebedragen. Hierbij kan worden uitgesplitst naar de situatie voor en naar de stuatie na de aanpassing.
Het gaat er bij Means om dat statistieken van een scale variabele worden berekend, eventueel uitgesplitst naar een categorische variabele, meestal een nominale variabele. Gemiddelden en standaarddeviaties uit laten rekenen is alleen zinvol voor scale variabelen. SPSS 20 echter rekent deze ook uit voor nominale en ordinale variabelen. Aan de gebruiker is het dan om de interpretatie op een correcte wijze te doen.

Bijvoorbeeld:

Hier worden voor de schadebedragen enkele statistieken uitgerekend. Daarbij is er uitgesplitst naar moment van de schade, dus of vóór en na de aanpassingen.

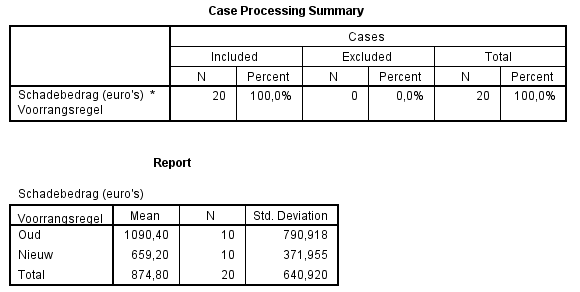
Te zien is dat het gemiddelde van de schadebedragen in de oude situatie ongeveer €430 hoger ligt dan het gemiddelde van de schadebedragen in de nieuwe situatie.

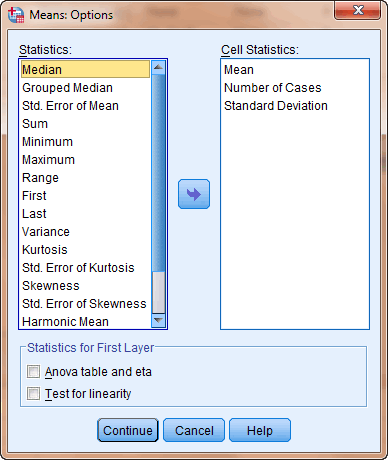
Hier zijn nu alleen Mean, N (Number of cases) en Std. Deviation bepaald. Bij Options in het menu bij Means staat een uitgebreide lijst met statistieken waaruit gekozen kan worden.

One-Sample T test

Het voorbeeldbestand bij One-Sample T Test
Het bestand bevat gegevens van 39 studenten. Van deze 39 studenten is hun woonsituatie, hun gelslacht en het tentamencijfer voor een specifiek tentamen bekend. Deze studenten zijn een steekproef uit een vrij grote populatie (N = 2000).

Met de One-Sample T Test wordt het steekproefgemiddelde berekend van één variabele én vergeleken met het gemiddelde in de populatie. Dat gemiddelde van de populatie komt uit een aanname/bewering.
Aan de hand van het steekproefgemiddelde wordt die bewering verworpen of geaccepteerd. Van tevoren wordt er een betrouwbaarheid gekozen voor de uitspraak over het al dan niet verwerpen van de bewering. Meestal wordt een betrouwbaarheid van 95% gekozen.

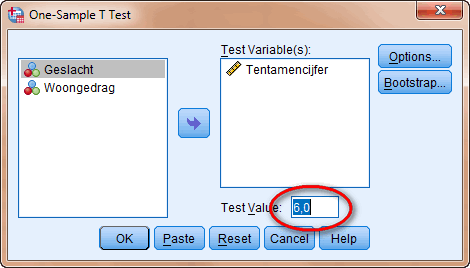
In het voorbeeld zijn de tentamencijfers bekend van 39 studenten. De docent beweert dat het gemiddelde cijfer voor dat tentamen een 6,0 is. Deze bewering wil hij toetsen door middel van een One-Sample T Test.

Voorbeeld:

Het resultaat in de uitvoer is:

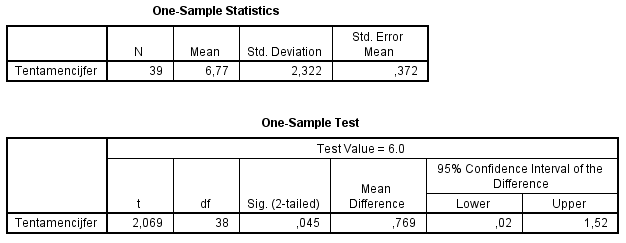
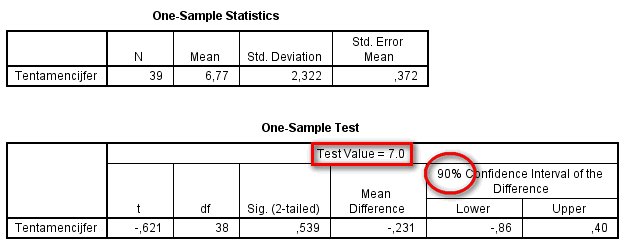
In de bovenste tabel staan enkele statistieken van het tentamencijfer. Het gemiddelde cijfer van de 39 studenten is 6,77. Om zich al duidelijk meer dan de 6,0 die getoetst gaat worden.
In de onderste tabel staat dat het verschil 0,769 is. Aan de hand van de vermelde significantie kan er dan getoetst worden ( Toetswijze 1 ). Daarnaast is het 95%-betrouwbaarheidsinterval voor het verschil vermeld. Hier wordt het verschil bedoeld tussen steekproefgemiddelde en de Test Value. Ook dit kan gebruikt worden voor de toets (Toets 2).

In dit voorbeeld betekent dit de volgende stappen en conclusies:

Toetswijze 1

H₀:    Het gemiddelde van alle cijfers voor het tentamen = 6,0.
H₁:    Het gemiddelde van alle cijfers voor het tentamen ≠ 6,0.

Neem een betrouwbaarheid van 95%, vergelijk de Sig. daarom met 0,05. De significantie is 0,045, dus kleiner dan of gelijk aan 0,05. H₀ wordt daarom verworpen. Dat wil zeggen dat het gemiddelde cijfer voor het tentamen significant verschilt van 6,0 (α = 5%).

Toetswijze 2

H₀:    Het gemiddelde van alle cijfers voor het tentamen = 6,0.
H₁:    Het gemiddelde van alle cijfers voor het tentamen ≠ 6,0.

Neem een betrouwbaarheid van 95%. Bekijk het 95%-betrouwbaarheidsinterval voor het verschil en onderzoek of de waarde 0 erbinnen ligt.  In dit geval ligt de waarde 0 niet in het 95%-betrouwbaarheidsinterval. Dat wil zeggen dat het gemiddelde cijfer voor het tentamen significant verschilt van 6,0 (α = 5%). Deze laatste toetswijze is wat betreft redenering wat lastig. Makkelijker wordt het als voor de Test Value 0,0 genomen wordt en onderzocht wordt of het populatiegemiddelde dat wordt getoetst binnen het 95%-betrouwbaarheidsinterval ligt.

Opmerking

Voor de Test Value kan een andere keuze gemaakt worden. Die hangt of van de hypothesen die getoetst worden. Bij Options kan er voor andere betrouwbaarheden worden gekozen. Als er bijvoorbeeld met een betrouwbaarheid van 90% getoetst wordt of het gemiddelde tentamencijfer significant afwijkt van 7,0 gaat dat op de volgende manier:

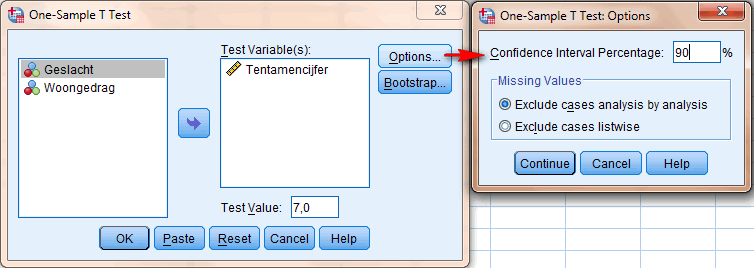
Het resultaat in de uitvoer is:

Concusies zijn aan de bezoekers van deze website.

Independent-Samples T Test

Het voorbeeldbestand bij Independent Sample T Test
Het bestand bevat schadebedragen bij ongelukken voor en na een aanpassing van een voorrangsregel bij een kruispunt. Voor de aanpassing wordt de oude situatie genoemd, na de aanpassing wordt de nieuwe situatie genoemd.

Met de Independent Sample T-Test worden van twee onafhankelijke steekproeven de twee steekproefgemiddelden berekend en met elkaar vergeleken. Verondersteld wordt dat deze aan elkaar gelijk zijn; gekeken wordt dan of de geconstateerde verschillen tussen die twee gemiddelden significant zijn. De interpretatie van de uitvoer gaat in een tweetal stappen.

In het voorbeeld staan tien schadebedragen vóór de aanpassing en tien schadebedragne na de aanpassing. Er is echter geen relatie tussen de schades voor en na. Vandaar dat het onafhankelijke steekproeven zijn.

Voorbeeld:

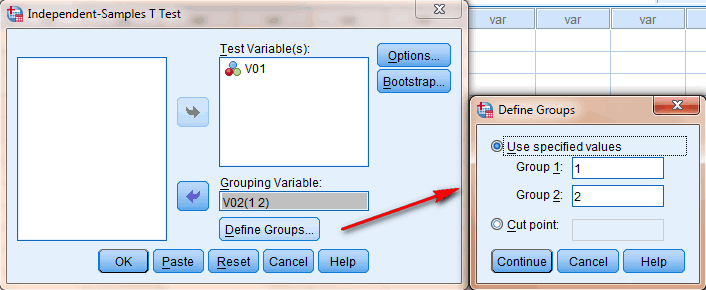
Het resultaat in de uitvoer is:

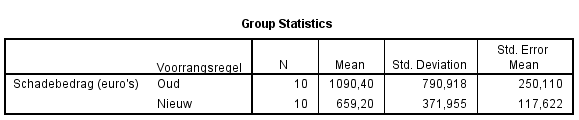
Het bovenste tabelletje bevat vrijwel hetzelfde als bij Means.
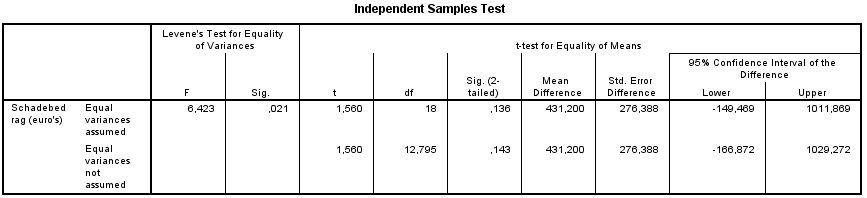
De onderste tabel bevat twee toetsen die beide gedaan moeten worden om conclusies te mogen trekken.

Toets 1

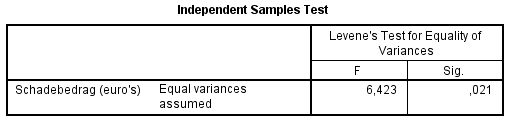
Toets 2

Bij toets 2 staan twee rijen in de tabel. Welke rij genomen moet worden hangt af van de uitkomt van toets 1: als bij toets 1 de nulhypothese geaccepteerd wordt moet de bovenste rij worden genomen. Als bij toets 1 de nulhypothese verworpen wordt moet de onderste rij worden genomen.

In dit voorbeeld betekent dit de volgende stappen en conclusies:

Toets 1

H₀:    De varianties in beide populaties zijn gelijk.
H₁:    De varianties in beide populaties verschillen van elkaar.

Neem een betrouwbaarheid van 95%, vergelijk de sig. daarom met 0,05. De significantie is 0,021, dus kleiner dan of gelijk aan 0,05. H₀ wordt daarom verworpen. Dat wil zeggen dat de varianties in beide populaties significant van elkaar verschillen (α = 5%). De varianties mogen dus niet als gelijk worden verondersteld.

Gevolg is dat voor toets 2 de onderste (rood omlijnde) rij moet worden gebruikt.

Toets 2

H₀:    De gemiddelden in beide populaties zijn gelijk.
H₁:    De gemiddelden in beide populaties verschillen van elkaar.

Neem de onderste rij en neem een betrouwbaarheid van 95%, vergelijk de sig. (2-tailed) daarom met 0,05. De significantie is 0,143, dus groter dan 0,05. H₀ wordt daarom geaccepteerd. Dat wil zeggen dat de gemiddelden niet van elkaar verschillen (α = 5%).

Vertaald naar het voorbeeld betekent dit dat, hoewel de gemiddelde schadebedragen na de aanpassing van de verkeerssituatie lager zijn dan die voor de aanpassing van de verkeerssituatie, er niet kan worden gesproken van significant verschillende gemiddelde schadebedragen. (Bij een betrouwbaarheid van 95%.)

Alternatieve aanpak van toets 2

Behalve naar de gemiddelden te kijken kan er ook naar het verschil van de gemiddelden worden gekeken. De beide hypotheses kunnen dan worden herschreven. Het betrouwbaarheidsinterval van het verschil kan dan gebruikt worden om de nulhypothese te handhaven of te verwerpen: als het getal 0 binnen het betrouwbaarheidsinterval ligt moet de nulhypothese worden worden gehandhaafd. Als het getal 0 niet binnen het betrouwbaarheidsinterval ligt moet de nulhypoyhese worden verworpen.

In dit voorbeeld betekent dit de volgende stappen en conclusies voor toets 2:

H₀:    Het verschil van de gemiddelden in beide populaties = 0.
H₁:    Het verschil van de gemiddelden in beide populaties ≠ 0.

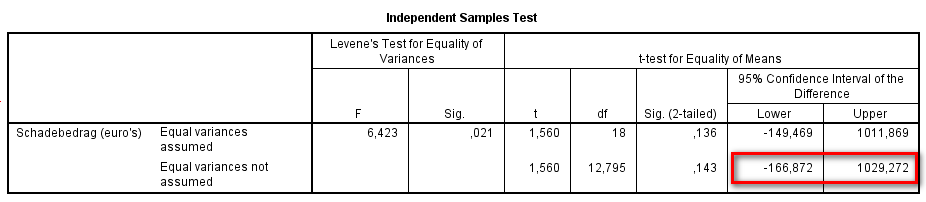
Neem de onderste rij. Hier is een betrouwbaarheid genomen van 95%. Het interval loopt van -166,972 tot 1029,272. Het getal 0 ligt daarbinnen. H₀ wordt daarom geaccepteerd. Dat wil zeggen dat het verschil van de gemiddelden gelijk aan 0 is (α = 5%).

Vertaald naar het voorbeeld betekent dit dat, hoewel de gemiddelde schadebedragen na de aanpassing van de verkeerssituatie lager zijn dan die voor de aanpassing van de verkeerssituatie, er niet kan worden gesproken van significant verschillende gemiddelde schadebedragen. (Bij een betrouwbaarheid van 95%.)

Opmerking 1: als er zoals zojuist beschreven getoetst wordt kan er ook getoetst worden of bijvoorbeeld het verschil significant anders is dan €300. Kijk dan of €300 binnen het betrouwbaarheidsinterval voor het verschil ligt.

Opmerking 2 bij het toetsen met andere betrouwbaarheden kan bij Options in het menu van Independent Sample T Test gekozen worden voor de gewenste betrouwbaarheden. Uitdraaien hierbij zijn:

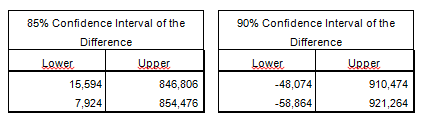
Paired Sample T Test

Het voorbeeldbestand bij Paired Sample T Test

Met de Paired Sample T-Test worden van twee afhankelijke steekproeven de twee steekproefgemiddelden met elkaar vergeleken. Twee steekproeven zijn afhankelijk van elkaar als het gaat om paren metingen, bijvoorbeeld bij het meten van het effect van een medicijn waar bij proefpersonen de situatie vóór en de situatie na wordt gemeten. Bij elke proefpersoon is dan een tweetal meetgegevens beschikbaar.
In het voorbeeldbestand is van een aantal echtparen bekend hoeveel geld per jaar aan kleding uitgegeven wordt. De uitgaven van de man en de uitgaven van de vrouw kunnen dan met elkaar vergeleken worden. Per echtpaar is dan een tweetal gegevens bekend.

In essentie worden bij afhankelijke t-toetsen per paar de verschillen berekend. Op deze verschillen wordt de One Sample T Test uitgevoerd. In het databestand zit ook een variabele voor het verschil. Doe eens de One Sample T Test met die variabele om een vergelijking te kunnen maken met de Paired Sample T Test.

Voorbeeld:

Het resultaat in de uitvoer:

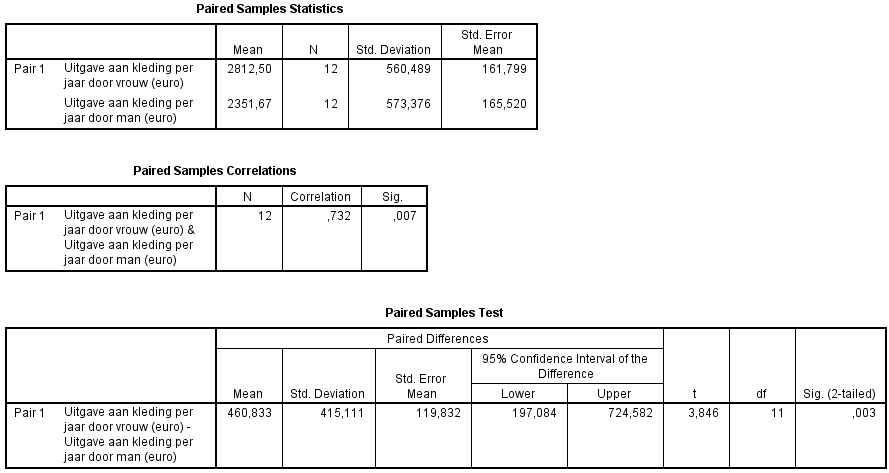
In de bovenste tabel staan wat enkelvoudige statistieken.

In de tweede tabel wordt de correlatie getoetst. Hier is een correlatie gevonden (r=0,732) die met een significantie van 0,007 sterk significant is. Hier betekent dat, dat wanneer bij een echtpaar de man veel geld aan kleding uitgeeft de vrouw ook veel geld aan kleding uitgeeft. Wat op zich niet zo bijzonder is, omdat goed zou kunnen zijn dat het gemiddelde gezinsinkomen bepaalt wat een echtpaar te besteden heeft aan kleding. Een hoog gezinsinkomen betekent dan dat zowel de vrouw als de man meer uit kunnen (en wellicht zullen) geven aan kleding.

In de onderste tabel staan de gegevens voor de toets.
In dit voorbeeld betekent dit de volgende stappen en conclusies:

Toets

H₀:    Het verschil tussen de gemiddelde uitgave aan kleding van mannen en de gemiddelde uitgave aan kleding van vrouwen = 0.
H₁:    Het verschil tussen de gemiddelde uitgave aan kleding van mannen en de gemiddelde uitgave aan kleding van vrouwen ≠ 0.

Neem een betrouwbaarheid van 95%, vergelijk de Sig. (2-tailed) daarom met 0,05. De significantie is 0,003, dus kleiner dan of gelijk aan 0,05. H₀ wordt daarom verworpen. Dat wil zeggen dat de gemiddelde uitgaven aan kleding van mannen en de gemiddelde uitgaven aan kleding van vrouwen significant van elkaar verschillen (α = 5%).

One-Way ANOVA

Het voorbeeldbestand bij One-Way Anova.

In het voorbeeldbestand staan de leeftijden (v27) en de wijken van afname van 110 respondenten. Voor het gemak wordt ervan uitgegaan dat het een representatieve steekproef betreft van de inwoners van de betreffende wijken.

Met One-Way Anova kan getoetst worden of de gemiddelde leeftijden in die vier wijken signicifant van elkaar verschillen. Als er twee wijken met elkaar vergeleken worden via One-Way Anova wordt in feite de Independent sample T-test uitgevoerd. Dan zijn er twee onafhankelijke steekproeven. Met drie of meer onafhanelijke steekproeven biedt One-Way Anova een oplossing.

Voorbeeld:

Hier wordt een eenvoudige Anova-analyse gedaan om het principe toe te lichten. Tevens wordt een grafiek gemaakt die (hopelijk) verduidelijkt hoe de redenering achter Anova zit.

De variabele leeftijd (v27) wordt hier uitgesplitst naar wijk. Bij Options wordt onderstaande keuze gemaakt:

Het resultaat:

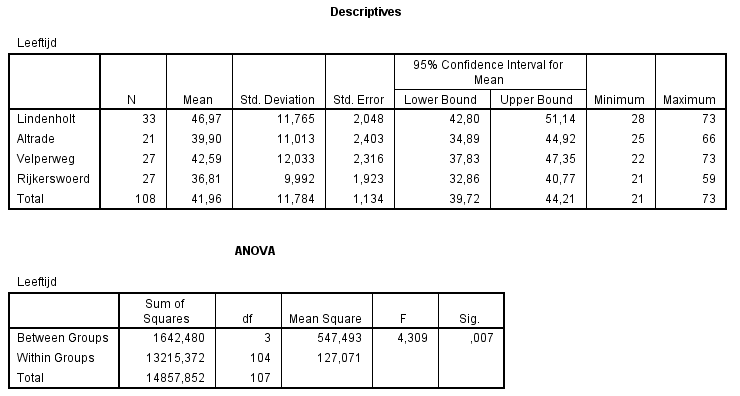
In de bovenste tabel staan wat statistieken van de leeftijden per wijk. Inhoudelijk wordt hier zodadelijk iets over geschreven.
De onderste tabel bevat de gegevens van de One-Way Anova toets.
In dit voorbeeld betekent dit de volgende stappen en conclusies:

Toets

H₀:    De gemiddelde leeftijden per wijk verschillen niet van elkaar.
H₁:    De gemiddelde leeftijden per wijk verschillen wel van elkaar.

De onderste hypothese zegt eigenlijk dat één of meerdere gemiddelden significant afwijkt/afwijken van de andere gemiddelden.

Neem een betrouwbaarheid van 95%, vergelijk de Sig. daarom met 0,05. De significantie is 0,007, dus kleiner dan of gelijk aan 0,05. H₀ wordt daarom verworpen. Dat wil zeggen dat de gemiddelde leeftijden per wijk significant van elkaar verschillen (α = 5%).

Korte toelichting

Om de One-Way Anova nader toe te lichten is als volgt een error bar gemaakt:

Resultaat:

Met wat aanpassingen:

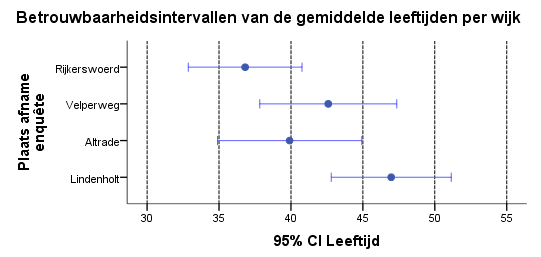
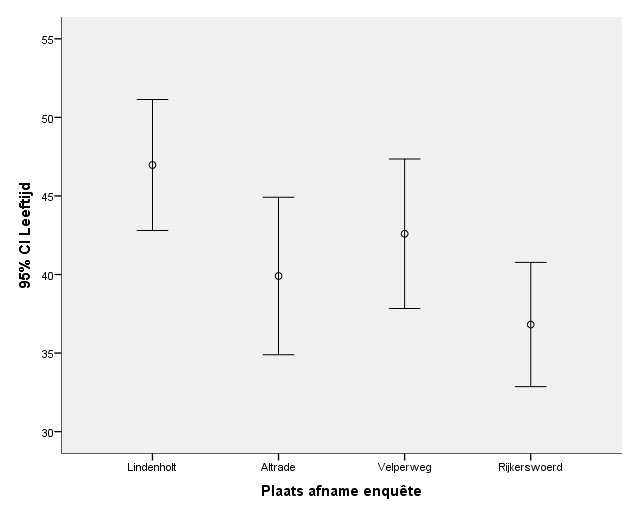
In bovenstaande grafiek vind je dezelfde gegevens (nu grafisch) terug als in een eerdere tabel. Die tabel staat hieronder.

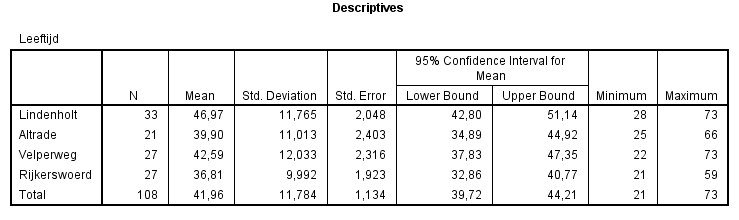
Voor Altrade is 95%-betrouwbaarheidsinterval voor de gemiddelde leeftijd: [34,89 ; 44,92]. In de afbeelding is dat ook af te lezen.

Als de nulhypothese geldt zullen de gemiddelden min of meer gelijk zijn en zullen de error bars min of meer boven elkaar liggen. Hoe meer de gemiddelden van elkaar verschillen, hoe verder de errorsbars van elkaar af zullen komen te liggen. Op een gegeven moment liggen de error bars zo ver van elkaar dat de nulhypothese zal moeten worden verworpen en de alternatieve hypothese moeten worden aangenomen.

In dit voorbeeld liggen de errors bars bij Rijkerswoerd en Lindenholt ver uit elkaar: ze overlappen elkaar helemaal niet. Dit wijst erop dat de gemiddelde leeftijden per wijk van elkaar kunnen verschillen.

Voor de uiteindelijke conclusie zal toch de One-Way Anova toets moeten worden gedaan, waarbij dan gekeken wordt naar de significantie.
Hier past het vermoeden bij de uitkomst van de toets.